入口 ＞トップメニュー ＞ワインとＣＧと祈り ＞現ページ

娘の宿題その２：正多面体が５つしかない理由　　(2018年1月24日記載)

　昨夜、娘にまた宿題を教えてくれ、と言われる。数学であれ、社会であれ、英語であれ、難しい宿題は、ママでなく何故か全部パパ(汗)。
　数学は、夏の「円周率を求めよ(なぜ３.１４なのか？)⇒詳しくはこちら！」に引き続き、今回は「正多面体が５つしか存在しない理由を書け」である。ええ～！？そんな問題、僕の中学生の時にあったかぁ？
　娘の教科書を見ずに、また脳みそ絞りましたよ～(汗)。 パパは、文系出身ですよ？突っ込みどころ満載かと思いますが、皆さま見逃してくださいm(__)m



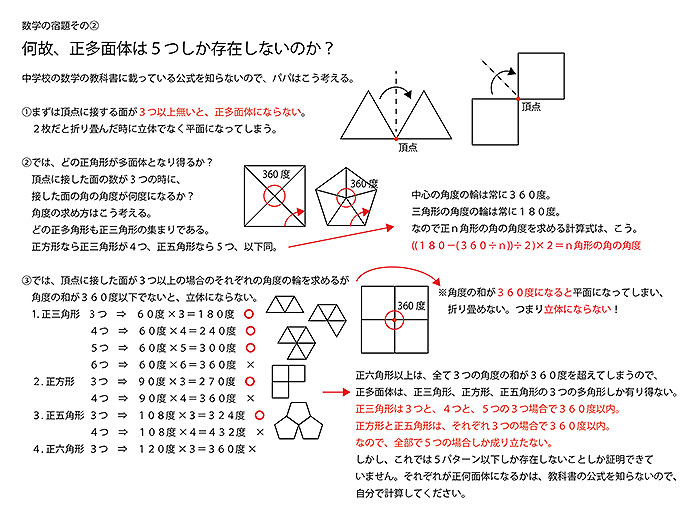
上の内容をざっくりまとめると、
①まず正多面体は、頂点に接する面が３つ以上ないと成立しない。２つだと折り畳むと平面になる。
②正多角形が頂点に接する角度は、全部で３６０度より少ないと正多面体は成立しない。３６０度だと完全な平面なので折り畳めない。(※３６０度を超えてしまうと、正多角形を曲げない限り多面体にすることはできない)。
③この条件で考えると、正六角形以上は３つの角度の和が３６０度以上になってしまうので、正多面体を構成するのは、正三角形と正方形と正五角形だけである。
④正三角形が、頂点に接した角度の和が３６０度以下になるのは、３枚と、４枚と、５枚の３種。正方形と正五角形では、それぞれ３枚の１種のみ。つまり全部で５種しかないと言うことである。

以上だけど、これはまだ正多面体を構成する要素が３タイプの正多角形で５種しかないことを示すに過ぎない。正多面体は、仕事のＣＧなら５つとも簡単に作れてしまうけど、それでは意味がないので。それぞれ何多面体になるかは、学校で習った公式に当てはめて計算してもらいます。
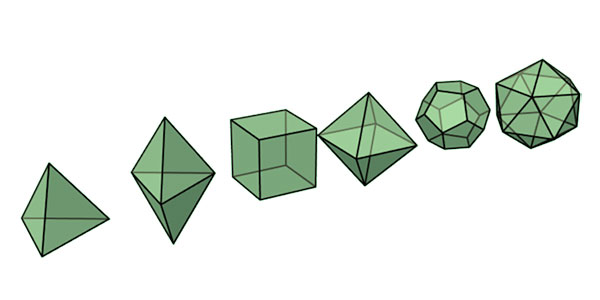
ちなみに正解は、正４面体(正三角形で構成)、正６面体＝立方体(正方形で構成)、正８面体(正三角形で構成)、正１２面体(正五角形で構成)、正２０面体(正三角形で構成)です。



で、３ＤＣＧで正多面体をモデリングしたのですが、
正三角形でも正６面体ができてしまった。
私は間違っているのだろうか？？

２０１８年１月２４日追記：友人より次のコメントをいただいて納得！腑に落ちました(^^)
正三角形の正六面体は「すべての頂点において接する面の数が等しい」にあてはまらないから正多面体とみなされないのでは？