入口 ＞トップメニュー ＞ワインとＣＧと祈り ＞現ページ

パパの夏休みの宿題：円周率π(パイ)　　(2017年8月20日記載)

　１８日金曜日の夕飯後、娘が「自由研究で円周率を延々と計算しようかな。3.14・・・と時間の続く限り計算するの。」と言った。「えっ？円周率を求める計算式知ってるの？」と驚くパパ。「小学校で習ったよ」。「いや、習ってないと思うよ。円周率を求めるのは凄く難しんだよ。パパにはできない」。「できるよ、習ったもん！」一歩も引かない娘。どうやら「円周÷直径」を言わんとしているらしい。パパがどう説明しても「できるよ！パパ、馬鹿になったの？」の一点ばり。
　う～ん、困った。どう説明しても納得しないし、一歩も引かない娘。パパは文系だし確かにお馬鹿かもしれないが、円周率の求め方の基本的な考え方ぐらいは分かる。娘はどう言っても納得せず、最後はふてくされて怒って寝てしまった。
　娘の就寝後、パパなりの円周率の求め方の考えをさらっとＰＣで書いて、テーブルの上に置いておいた。明日、これ読んだら少しは理解するかな？(笑)。



　で、金曜の話しの続きである。娘の主張は「小学校でメジャーで円周を測った！で、円周を直径で割った！」であった(笑)。そんなことだろうと思った。
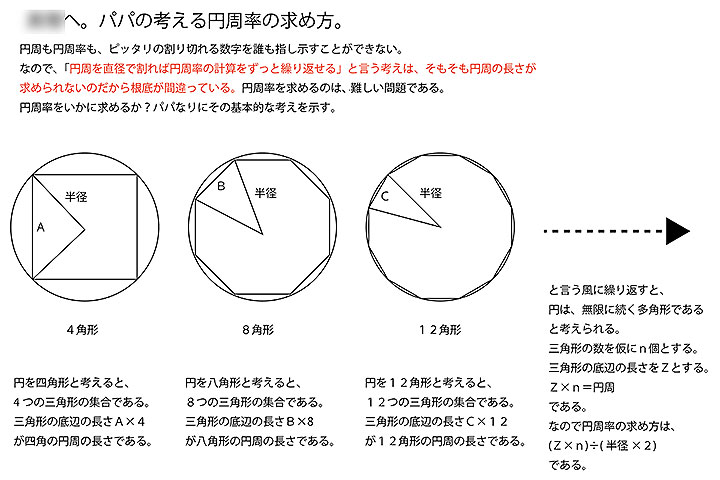
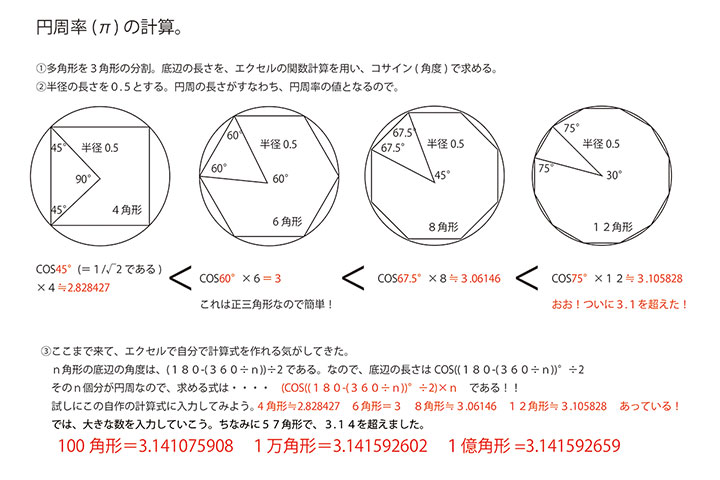
　それはそれとして、個人的に円周率と円周をどう求めたらよいか、２日経った日曜の今日(２０日)の夕方、１時間ほど考えてみた。先日の基本的な考え方は間違っていないと思うので計算してみる。「円は無限の多角形(無限の２等辺三角系の集合体)である」と言う考えに従って計算する。関数電卓を持っていないので、ＥＸＣＥＬの関数計算を使用する。半径は０.５とした。円周がそのまま円周率の数値となるので。まず、４角形かスタートして、６角形、８角形、１２角形と進んでいった。６角形だけは、正三角形が６つ集まったものなので、ＥＸＣＥＬを使わずともすぐに分かる。さて、１２角形まで計算して「こりゃ、計算式作れるよね？」と思って、トライしてみた。ｎ角形を三角形に分割。２等辺三角形の各角度は簡単に求められるので、底辺の長さはコサインで計算。それをｎ角形の数でかければ円周、すなわち円周率が分かる。ネットでいっさいググらずに、自力で作った計算式が、

π＝(COS((180-360÷ｎ))°÷2)×ｎ

円周率のパパ計算式完成！
※ＥＸＣＥＬでＣＯＳを求めるときは、ＲＡＤＩＡＮＳを使うので、ＥＸＣＥＬでの式は下記になります。

=COS(RADIANS((180-(360/A1))/2))*A1　(A1は、A列の1行目にｎ角形のｎを入力したことを示します)。

　数値を入力する。５７角形で３.１４を超えた。１万角形や１億角形のレベルになると、３.１４１５９２６まで同じで、それ以下の小数点が変化していく(僅かずつ増えていく)。「無限」と言う数を入力はできないので、１億角形で終了。理系の方が見たら突っ込みどころ満載なのかもしれませんが(笑)、文系パパの夏休みの宿題はこれでおしまい！意外と楽しかったです(^^)